Are We 84.7% Certain We're in the 90th Percentile?
Of course, hospitals should focus on patient satisfaction. That's important but is often a vague and uncertain thing to measure. But, as Dr. Deming said:
“The most important figures that one needs for management are unknown or unknowable (Lloyd S. Nelson, director of statistical methods for the Nashua corporation), but successful management must nevertheless take account of them.
When hospitals attempt to quantify patient satisfaction, there are some things that can be done to make those numbers more meaningful to patients and staff members alike.
I was recently in a hospital that posted a number of performance measures, a balanced scorecard of sorts. One measure was the percentage of surveyed patients who said they would recommend the hospital to others.
That section of the board said, basically:
Actual = 84.1%
Target = 86.5%
The yellow indicates that the actual percentage was lower than the target.
So what does this mean? For one, if the target had been set at 83.9%, things would have been green. So, what does that mean to patients or staff?
Regardless of the target and however it was set, the actual is what it is.
As a patient, how do we know if 84.1% is good or not? How does it compare to other hospitals? Do the staff members even know if this is “good” or not?
Many hospitals set a goal of being in the 90th percentile of certain measures, including patient satisfaction. Why not aim for perfection? How do leaders decide that it's OK for 13.5% of patients to NOT recommend the hospital? It seems like a completely arbitrary and meaningless number, that goal.
Thinking back to my days in manufacturing, companies often confused “specification limits” with the “voice of the process.” Spec limits might be set based on real customer requirements or they might be completely arbitrary. A key lesson of Dr. Deming and Dr. Donald Wheeler is that we need to, as leaders, react to the voice of the process, and we need to, as Dr. Wheeler points out so eloquently in his book Understanding Variation: The Key to Managing Chaos
One of the flaws in posting a single number (84.1%) and comparing that to the goal (86.5%) is that we have no context of trends over time.
Some organizations might compare this most recent period to last quarter or last year. Again, Wheeler points out that a comparison of two data points isn't statistically significant, as two data points don't make a trend. If the number is higher (or lower) than last year, we don't necessarily know what action to take. Organizations often over-react to every up and down in a performance measure, even if that up or down is noise in the system.
Run Charts Are Better Than Single Data Points
If a hospital presented the “Would you recommend?” data as a time series chart, patients and staff could tell much more.
As Wheeler points out, we can get far more information (and make better management decisions) based on a run chart and time series data – far better than that simple comparison to a target or a comparison to last year.
Let's look first at a simple run chart (with made up data). Is patient satisfaction improving? At first glance, we might say “yes, it's getting worse, there is a clear trend.” It used to be in the 90%+ range, now it's only 84%. It's fallen three months in a row. Time to take action! Send out a memo, meet with the leadership team – kick some butt and make things better.
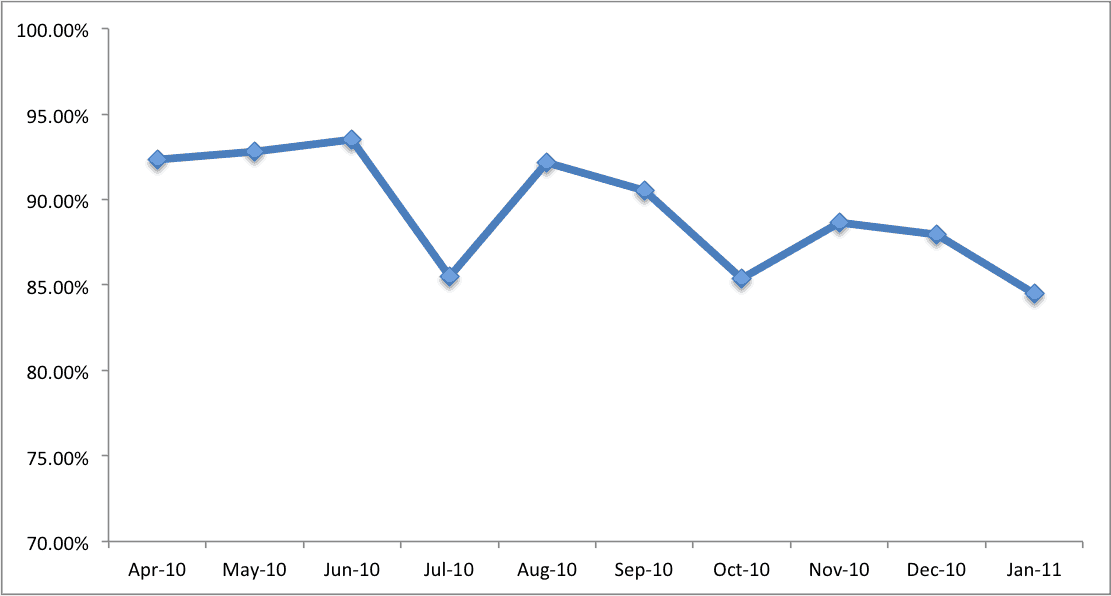
Some analysts might add a linear trend line to the chart – it's statistical and it's easy to do with a few clicks in Excel. That linear trend is clearly downward – things must be getting worse! Or are they? Call a committee or task force together, publish an exhortation to improve in the employee newsletter. Give an inspirational speech at an all hands meeting. Take action!
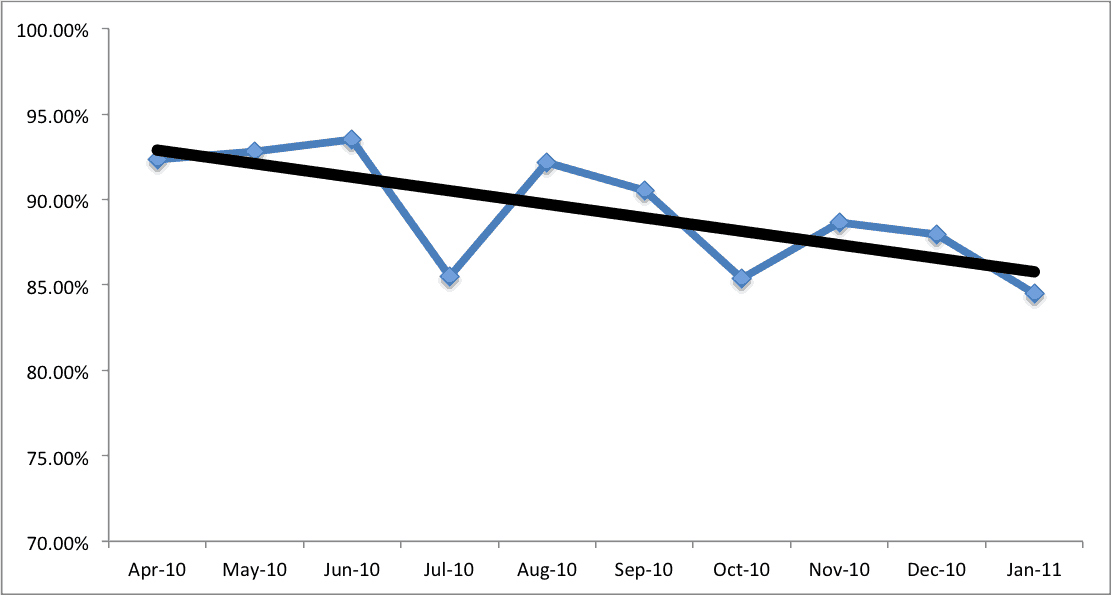
The punchline behind the data I've presented above is that it's randomly generated, a normal distribution around an average of about 89%.
As Deming and Wheeler point out, we have to, as managers, learn how to separate “signal” from “noise.” The mean and the data points are the “voice of the process.” This data shows what our current process and system is capable of. If management sets a “target” of 95%, that's meaningless – the system is not capable of hitting that target on an ongoing basis. SPC teachers would tell us to not even put the target on the chart – don't confuse a “specification limit” with the voice of the process.
The target is just a target. If we could just boost performance by setting a target and giving incentives, everything in healthcare would be fixed already (and in business, for that matter).
If we have a stable patient care and service process, a stable hospital where the team and processes and environment are roughly the same each month, there's going to be common cause variation around this mean or average percentage of patients who would recommend.
Some months, we might have 94% patient satisfaction, and some months, we might have 84% patient satisfaction – and it doesn't mean anything is necessarily BETTER or WORSE in the system. Any of these fluctuations might just be noise – meaning there's nothing to react to. Dr. Deming warned against “tampering” with a stable system, meaning that if we react to every little up and down in the patient satisfaction scores, we are bound to make variation in that number WORSE than if we just left things alone.
I'm not saying “don't try to improve” – what I'm saying (as I learned from reading Deming and Wheeler) is that we can't (shouldn't) overreact and make false judgments based on the data.
SPC Thinking
We need to use SPC (statistical process control) thinking.
If we look at the data with a simple mean line drawn, it looks like this:
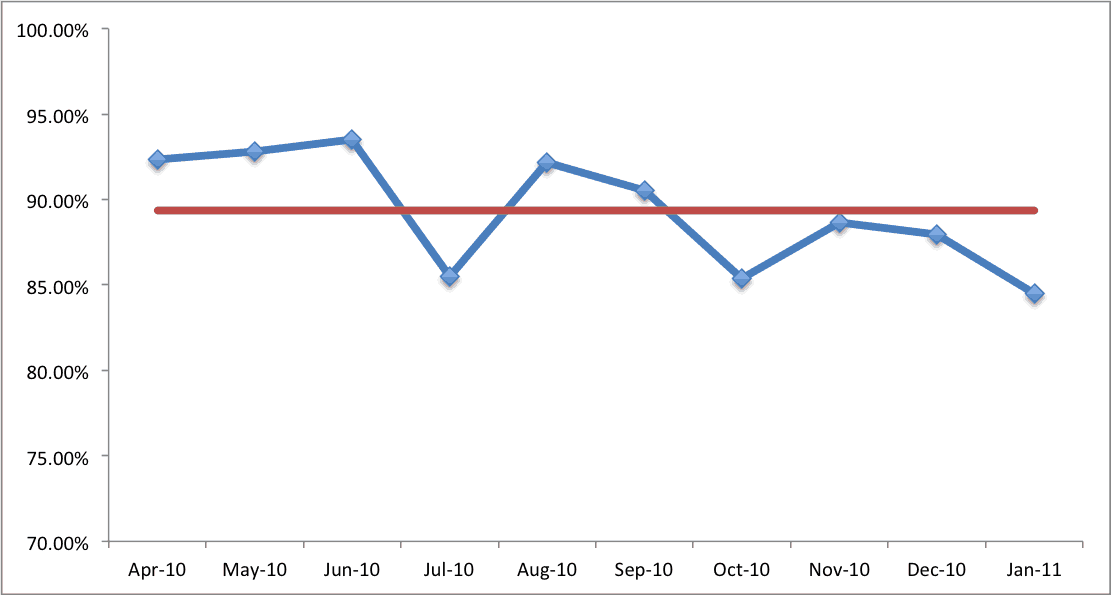
It becomes more visually clear that basically half the data points are above average, and half are below average. This is completely predictable from a statistical standpoint – again, it's just noise.
At a conference last week, I saw a presenter show some data and he said, a bit exasperated, “The numbers keep going up and down.” The common cause variation kept the data moving between about 85% and 95% – just like my made up data set here.
Using the standard SPC rules, we CAN make certain determinations that things have gotten worse or better statistically. If we have eight data points in a row ABOVE the old average, we can say that's not a random chance. Something has changed in the system that has boosted patient satisfaction in a meaningful way. We call this a “special cause.” As leaders, we need to then go understand WHAT changed – how do we capture that learning as an organization? If we have eight data points in a row BELOW the mean, we can say things have gotten worse – again, why and what can we do about it?
Using SPC rules like this (see a complete list here) can help management avoid reacting to noise and avoid tampering. It allows us to focus our efforts to work on important issues, rather than just chasing normal variation.
Now let's look at an SPC chart that includes “+/- 3 sigma” upper and lower control limits:
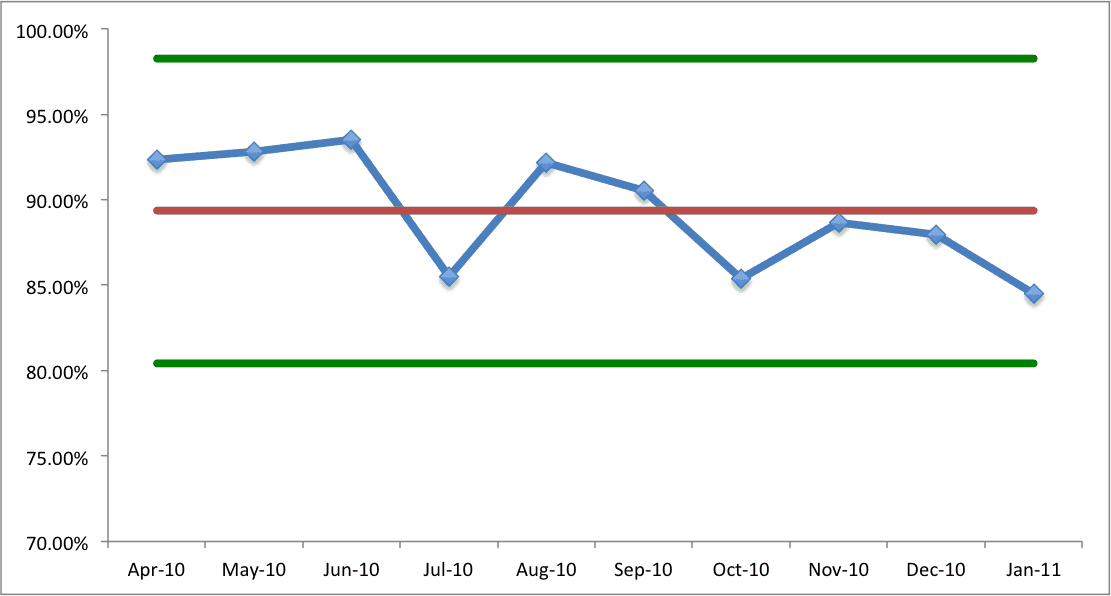
The calculations of the control limits tell us that any single data month between about 80% and 98% percent is likely to be just noise, or common cause variation. A single month of 96% is bound to happen, by chance, statistically. We could throw a huge party, give bonuses to employees and, guess what, the next month things will tend to regress to the mean. Satisfaction might now be just 90%. Still above our “target” (which, to me, is pretty meaningless, this target) and it's still better than the mean. Things aren't getting worse – they are just fluctuating.
Now, there are currently four consecutive points below the mean – if there are four more consecutive data points below the mean, then there would be a statistically significant shift downward – a special cause.
If we have any one single point outside of these control limits, that's statistically significant – there's a special cause to go investigate in a good way or a negative way. Again, there are other more detailed SPC rules that you can reference, but understanding just a few basic rules and putting data in a simple run chart can go a long way toward avoiding some very common (and costly) management errors.
Update: Read more in my 2018 book, Measures of Success: React Less, Lead Better, Improve More.
What do you think? Please scroll down (or click) to post a comment. Or please share the post with your thoughts on LinkedIn – and follow me or connect with me there.
Did you like this post? Make sure you don't miss a post or podcast — Subscribe to get notified about posts via email daily or weekly.
Check out my latest book, The Mistakes That Make Us: Cultivating a Culture of Learning and Innovation:
Not to be too much of a purist… but from eye balling the chart there seems to be one special cause (or signal as Wheeler calls them) in this data set.
It seems observation 5 fails “Test 6” which is 4 out of 5 points more than 1 Stdev from CL (same side). If you send me the exact data I can tell you for sure! ;-)
Good catch. I had randomized data… so it’s possible that specific rule is being violated. So there could have been that period where things WERE better (did we understand why) and things weren’t sustained.
You’re absolutely right (and not being a purist) that we should use all of the Western Electric rules, not just mean and UCL/LCL tests.
I’m so glad to see a statistical discussion on here Mark! I think Lean gets too enamored with the other tools as to forget the power of statistics, and some people go as far as to think Lean has nothing to do with statistics (“That’s what those SixSigma people do!”). I view it as a form of visual management, and it should be a tool in every Lean practitioner’s bag of countermeasures.
So there’s a reason why that test is test #6 as opposed to #1: because it is less deterministic, and you proved that to be a fact. You have random data. There is no special cause. Failing any of the tests is just an indicator that there might be something to look at, but it is not certain, especially as you get to the higher numbered tests. I would hesitate to call these “rules”, as they are just tests of hypotheses. You can even have normal occurrences that are outside of the control limits that are not special cause (statistically speaking). We should just be mindful when using statistics, as it is never black and white. Your example was excellent at illustrating that point.
“So there’s a reason why that test is test #6 as opposed to #1: because it is less deterministic, and you proved that to be a fact.”
It’s either deterministic or probabilistic.
“I would hesitate to call these “rules”, as they are just tests of hypotheses.”
They are rules of thumb or heuristics. There is no use of test of hypothesis in control charts. See the difference between analytical and enumerative statistical studies.
“You can even have normal occurrences that are outside of the control limits that are not special cause (statistically speaking).”
Are you sure your are referring to control charts?
Correct me if I’m wrong, but having a single data point outside of the control limits is not a 100% indicator of a special cause being present. It’s more than likely, but not absolutely true.
Yes. A single point outside of CLs is a special cause and requires investigation. There’s no room for speculation.
Fernando, you are wrong on this. Control limits are calculated based on a balance between having them too tight and too loose. For an I/MR chart, the UCL is the mean + 3 * (average of the moving range) / 1.128.
There is a chance we have “alpha error” (type 1 error) where a single point being above UCL is *not* due to a special cause. There is also the chance of type 2 error that a single point is INSIDE the limits even though there is a special cause. This is sometimes referred to as a “false alarm.”
I’m lazily citing Wikipedia (which cites a statistics book):
“Data satisfying any of these conditions as indicated by the control chart provide the justification for investigating the process to discover whether assignable causes are present and can be removed. Note that there is always a possibility of false positives: Assuming observations are normally distributed, one expects Rule 1 to be triggered by chance one out of every 370 observations on average. The false alarm rate rises to one out of every 91.75 observations when evaluating all four rules.[6]”
The control chart rules are not hard set rules as in there IS a special cause. It’s an indicator that there is LIKELY a special cause.
Mark,
The alpha and beta errors you refer to, are the two possible mistakes one can make when making decisions ….without the use of a control chart. Use of a control chart provides an economic balance by reducing the risk of making either of these errors.
I liked your elaborate explanation and emphatic conclusion. It reminded me of 1988 when I espoused the same theory. However, both your explanation and conclusion are wrong because your choice of underlying theory is flawed.
You are using the theory used by advocates of the statistical approach. It states that the design and validity of the control chart relies on normally distributed data and that probabilities can be assigned to all chart zones. Hence, your use of probabilities for likelihood of false signals. All those probabilities are meaningless.
I ascribe to the theory founded on the Shewhart approach which is concerned with data homogeneity. If you want to move away from Wikipedia, and you would like to research further, the following book should prove invaluable:
Normality and the Process Behavior Chart by Donald J. Wheeler
“This book provides the first careful and complete examination of the relationship between the normal distribution and the process behavior chart. It clears up much of the confusion surrounding this subject, and it can help you overcome the superstitions that have hampered the effective use of process behavior charts.”
With respect to your statement, “The control chart rules are not hard set rules as in there IS a special cause. It’s an indicator that there is LIKELY a special cause.”
Donald J. Wheeler has this to say about that, “it will be economical to seek to identify and exert control over any Special Cause identified by a process behavior chart.”
Regards,
Fernando J. Grijalva
@demingsos (twitter)
Ok thanks. We are basically arguing a very minute and academic point that doesn’t change how I use control charts in practice. I will continue to assume that a point outside the 3 sigma control limits has a special cause even if I cannot be 100% sure that is the case. It is far better than the old practice of, say, reacting to every single data point that is worse than the mean.
Could the same be said of observation #6 also fails “Test 6” when looking at 6-10?
Great stuff, everybody. I was one who often ignored statistical analysis techniques in favor of practical lean tools, until I read the book Mark mentioned, “Understanding Variation.” Once I understood the signals of process behavior, and how to use a control chart to detect them, it all started to click. I’m still biased towards simple graphical depictions of data that folks without statistics training can intuit, but the control chart, and the capability 6-pack, are without a doubt part of my toolbox now.
Yes, I had to laugh, this looked very much like the Six Sigma which I didn’t think Mark was a fan of.
This is a big problem in my organization, managers are asked to comment on minor fluctations in their run charts that are well within control limits.
This is Waste 101 – managers trying to manage normal variation point by point, rather than developing improvements and measures to reduce overall variation that is outside customer spec.
My favorite example was a 36 point run chart where we asked the managers of this business to explain an overall trend upwards, a trend that was clear and linear. They responded by trying to explain every single one of the points (in May it was a union dispute, in June is was staff sickness, in July it was new laws passed, August was IT failure, September was the big office move, and on and on they went!!!)
Yes Richard, that time spending investigating and “explaining” common cause variation is a huge waste. I’m normally ambivalent toward six sigma programs, but I certainly use and advocate statistics and the basic QC. You can use SPC without a formal six sigma program and it’s belts and all. I believe that is Toyota’s approach, as well.
Did you know? “In the 1940s the War Production Board trained approximately 50,000 individuals in how to use process behavior charts (also known as control charts). ” Wheeler
Statistical Quality Control, which includes SPC, is a discipline that is and always will be independent of any improvement specific approach (six sigma, lean, TPS, etc.) It is really a part of the BOK of the Industrial and Systems Engineering profession.
Thank you, Mark.
One of the things that people forget when they get into keeping statistical records of events is that they can’t manage the numbers. They need to manage the process. Improving the process will get improved numbers, but the numbers will still move around.
I agree, Chet. I almost always see attempts to track all the numbers, in essence trying to collect population data on a particular metric. Maybe sampling should be utilized more often. Sampling, if done right, can provide quite reliable data at a fraction of the effort.
Also, going to the gemba to observe and get feedback is a critical activity that can provide just as much or more insight than data analysis.
Consider Deming’s advice when dealing with enumerative statistical studies.
“Test of hypothesis has been for half a century a bristling obstruction to understanding  statistical inference.”
“a confidence interval has no operational meaning for prediction, hence provides no degree of belief for planning.”
“Incidentally, Chi Square and other tests of significance, taught in some statistical courses, have no application here or anywhere.”
The indiscriminate use of enumerative studies was on the main reasons why Deming never supported Six Sigma.
Absolutely agree with Steve Harper – it’s good to see some statistics here.
Popular misconception about Lean is to copy Toyota way (or just extract some popular things like zero inventory or one-piece-flow) “just because”… Data driven decisions is a way to separate popular stuff from Lean approach.
Thanks for the comment, Konstantyn. Readers of this blog know that I don’t advocate blindly copying Toyota or any other organization – and certainly not to failed extremes like “zero inventory.”
Mark,
Thanks for reinforcing the importance of SPC. Unfortunately management will always, at least in my experience, demand that we set a lofty target to which we must strive. It is either arbitrary or we are told that “best-in-class” facilities achieve X% based upon industry studies. They’re fine will implementing SPC, but they still want a target.
As a lean practitioner, how do you go about actually calculating an achievable target that will satisfy management?
Please assume you HAVE to set a target. Management insists. ;-)
I’d set a “goal” of 100% satisfaction or zero errors.
I wouldn’t punish people for not hitting the goal.
That’s true north – working toward perfection. SPC tells us if our system and processes are at all capable or not.
Tricky question!
Take an example of GRR attribute: when you judge measurement system you consider result and lower limit. You also have 2 targets: for goal and for lower limit. Maybe it will be good to have the same for this case?
I don’t understand the question. Can you give an example?
I was talking about JM’s question. It’s quite difficult to change management point of view, regarding targets and bonuses. Any MBA guy will tell that you cannot work without a target. Set a target and follow the KPIs…
My comment is not a question – just idea. Against of using target value, use target limits.
Mark,
You write – “I’d set a “goal” of 100% satisfaction or zero errors.”
Consider that “100% satisfaction or zero errors” assume NO variation. As Deming stated, “perfection is not of this world” and “No system, whatever be the effort put into it, be it manufacturing, maintenance, operation, or service, will be free of accidents.”
Regards,
Fernando J. Grijalva
@demingsos (twitter)
100% ultimate perfection might not be possible, but that would still be my aspirational goal. My distinction with not calling it a “target” is that I’m not going to blame, punish, embarrass, or ridicule people if there is an error. We’re going to look at the system and identify improvements that lessen the risk of future error.
The voice of the process, statistically, might say that 2 patients are going to fall each month. The mean in the control chart allows us to predict that 2 are going to fall next month (+/- the variation that’s shown in the data). But I’m still going to work toward the goal of having ZERO falls.
I’m afraid the idea that “we can’t be perfect” becomes an excuse to not improve. I can’t imagine that’s what Dr. Deming would have wanted.
You state that, “100% ultimate perfection might not be possible, but that would still be my aspirational goal.”
As engineers, you and I should know, that achieving “100% ultimate perfection” is statistically and economically impossible in open socio-technical systems. It is an illusion that one can operationalize “aspirational goals” in order to develop “aspirational methods” for achievement of “real” improvements.
Aspirational goals are in the same category of slogans and exhortations… No method, no result, wishful thinking. Why waste resources pursuing this?
You write, “I’m afraid the idea that “we can’t be perfect” becomes an excuse to not improve. I can’t imagine that’s what Dr. Deming would have wanted.”
Understanding and accepting the constraints of a system does not mean abdication towards its continual improvement. For example, one of many possible improvement strategies, could be the redesign of the system in order to increase its MTBF. I don’t know what Deming would have wanted, but the validity of the theory in question is beyond Deming’s desires.
In summary, Zero defects, 100% ultimate perfection, or any other variation of the theme, only adds to the database of superstitious knowledge that continues to destroy the foundations of our institutions.
Regards,
Fernando J. Grijalva
@demingsos (twitter)
I think tolerating a certain number of patient infections as “inevitable” is far more damaging to institutions and society than wanting to aim for 100%. I don’t think that’s an empty slogan if you do (as we do) have a method for working toward that. I think you’re being too harsh, Fernando.
Mark,
Accepting the capability of a process does not equate with the toleration of undesired outcomes. Being aware that the system is incapable of achieving zero defects is even a more compelling reason for its critical management and further improvement. Don’t you think so?
Regards,
Fernando
I’d argue you can simultaneously be wanting to push toward 100% while being aware that the current system is incapable of that.
It’s like having a specification limit and a control limit. You don’t put the specification limit (zero patient falls) on the control chart and you don’t punish people for not having zero falls. If the lower control limit for patient falls is 1 per month, you are aware of that and you work on common causes in the system.
Here is a great example of not seeing enough data points to know if there is a statistically significant improvement:
See this chart on this page.
4 data points are better than 2, but what was the previous trend??
If the lower control limit for patient falls is 1 per month, you are aware of that and you work on common causes in the system. I don’t know what Deming would have wanted, but the validity of the theory in question is beyond Deming’s desires. As engineers, you and I should know, that achieving “100% ultimate perfection” is statistically and economically impossible in open socio-technical systems.
Julianne-
Scotland has reached “perfection” in terms of having zero central line infections in the entire country in March 2011. If one month, why not more?
http://adventuresinimprovingaccess.blogspot.com/2011/12/raising-expectations-in-healthcare.html